Prisoner's Dilemma

What is the Prisoner's Dilemma?

The Prisoner's Dilemma is one of the most famous game theory concepts, also commonly referred to as the "peace-war game". According to this concept, participants in a conflict or negotiation will, in most cases, refuse to cooperate, even if this cooperation allows them to achieve their interests. Thus, each participant seeks only to benefit themselves, which is today a major problem in politics, economics, business, the social environment, and all spheres of human life.

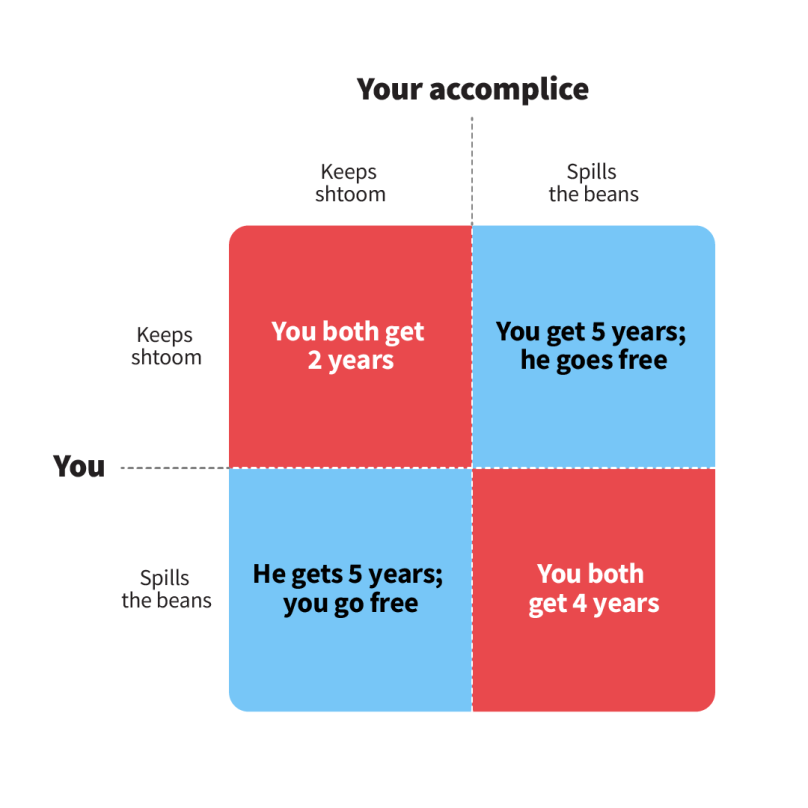
Thus, the Prisoner's Dilemma is an issue for which no universal approach exists. Instead, the dominant strategy in the Prisoner's Dilemma is the method that brings its user the most significant benefit regardless of other actors' game plan, forming the core of this dilemma. The famous allegory of two accomplice thieves caught by the police best illustrates this. Locked in separate cells, the accomplices cannot interact with each other. The policeman offers each prisoner three options in turn:

• Both accomplices keep silent until the last moment, and if no one confesses in the allotted time, both receive the shortest possible prison sentence.
• One accomplice turns in the other, the first is released, and the other gets the maximum sentence.
• Both accomplices turn each other in and receive the same punishment - a medium sentence.

Since the accomplices cannot interact with each other, neither of them knows what the other will do. Thus, the threat of being the only one who will go to serve a sentence (in the case of the second scenario) tends to force both accomplices to turn each other in. In the end, pursuing their interests, they receive a medium prison sentence, even though they could both have received the minimum sentence while remaining silent.

The definition of the Prisoner's Dilemma

To begin with, it is worth clarifying what game theory is to understand the Prisoner's Dilemma. Thus, game theory is a mathematical method of constructing behaviour strategy in any process involving two or more parties pursuing their interests. Since each side uses its tactics and tools and has a specific goal, each participant has an equal chance to win or lose. Game theory allows us to choose an advantageous mixed strategy based on understanding the other parties' psychology, thinking, and resources.

The American mathematician Albert Tucker formulated the Prisoner's Dilemma as a theory. He used it to illustrate the difficulties in games where there is only one prize, and many players do not want to work together. But why is this phenomenon called the "Prisoner's Dilemma"? It is all about the laws in most countries, which punish criminals if they set each other up or confess and often do not punish if both remain silent. This idea, together with the problem of cooperation, forms the basis of Tucker's theory of the prisoner's dilemma.

Here are its theoretical points:

• The prisoner's dilemma develops in situations where participants have motives to make the situation of the other participant worse. Yet, they don't have a conscious motive to improve the situation for everyone simultaneously.
• According to the Prisoner's Dilemma, an individual benefits the most when antagonising and betraying everyone else.
• With each repetition of the same game, the parties begin to encourage cooperation and gradually come to a mutual benefit.
• Despite the destructive motives and incentives that drive participants in a particular process to pursue their interests at the expense of others, the Prisoner's Dilemma can and should be overcome.

The importance of the Prisoner's Dilemma

Although the Prisoners' Dilemma is a game-theory discipline that is not widely known or even understood, it is also not uncommon in everyday life. For example, knowing how the Prisoner's Dilemma works helps:

• Choose the most effective tactic in a negotiation when it is not immediately clear whether to negotiate hard or soft;
• Manage a team and resolve internal conflicts;
• Do business when you must pick between self-interest and customer satisfaction;
• Make important decisions about your personal life when you have to choose between several options with different levels of benefits.

In summary, the prisoner's dilemma provides a way out of a difficult situation, or at least an insight into an opponent's motives and behaviour pattern, so as not to be caught off guard or take a decision at your peril.

The Nash equilibrium in the Prisoner's Dilemma

Nash equilibrium is another concept in game theory that sometimes arises in the context of a prisoner's dilemma. Nash equilibrium is a situation where increasing the winnings is not possible unilaterally. That is, a game (process) participant can only raise their winnings by changing their strategy if other participants don't change their strategies. Mathematician John Nash, who discovered this phenomenon, gives an example of wolves in the forest: wolves never eat all the hares because otherwise, they have no food left. As a result, agreeing that each wolf eats in moderation with the others is the most winning outcome of this 'game'.

There are also several possible variations of Nash equilibrium when there is an edge to one side or the other:

• A strict equilibrium - the player can change their strategy, but they will only make it worse for themselves and others;
• A weak equilibrium - if they change their strategy, they also create good conditions, but not better than they were before.

If the player can improve their position by changing the strategy, there is no Nash equilibrium.

Consider as an example a situation from everyday life. Suppose two cars are driving in two adjacent lanes but in opposite directions. How many equilibrium situations are there? First - both drivers are going on the right side of each other, and both remain safe, just passing each other. The second - one of the drivers changes course, and a serious accident occurs, resulting in what can be called a strict equilibrium scenario. The third, weak equilibrium, is when both drivers want to change the situation and do so in the same way, with the result that it is neither worse (no accident) nor better.

How to escape the Prisoner's Dilemma

Robert Axelrod, an American political scientist, found in his many years of research into the Prisoners' Dilemma that the more often people get confronted with the dilemma, the easier and faster they find a way out. It is facilitated by past experiences (usually negative experiences that have been present for everyone in this dilemma), new skills (conflict management and public speaking are particularly important to Axelrod) and achievements with valuable lessons learned from them. The scientist also found that strategies whose primary motive was greed led to worse results in the long run than strategies dominated by the desire for compromise and building friendly relations between the participants.

Based on this data, Axelrod identified several principles to help get out of the prisoner's dilemma or avoid it altogether:

• Negotiating strategies should not contain manipulation, and the participants should refuse to try to deceive their opponents unless they violate this principle.
• If one participant betrays the interests of the other, the second must reciprocate to stabilise the overall situation.
• Once the "revenge" has been carried out, the participants must return to cooperation and adhere to the first principle.
• The negotiation strategy should satisfy all interests equally, without seeking to outplay anyone and win more benefits.

Adhering to these principles has dramatically increased the effectiveness and outcome of negotiations in which a prisoner's dilemma has arisen. Thus, Axelrod's strategy has the best chance of benefiting all participants. The key is to overcome self-interest in favour of the common good, and to repeat the game more than once if it cannot be done immediately. Then, over time, participants can develop strategies that encourage cooperation and punish betrayal, reducing the incentives to betray.

There is also an alternative way of eliminating the prisoner's dilemma. It involves collectively creating tools and strategies to avoid disruptive incentives and to overcome stereotypical thinking in favour of rational, informed and mutually beneficial solutions. However, such a way out of the dilemma requires additional resource input and involving all participants in the development process.

One such tool is the prisoner's dilemma payoff matrix, a four-column matrix containing the following information:

• What happens if the first participant betrays the second?
• What happens if the second participant betrays the first?
• What happens if both participants betray each other?
• What happens if no one betrays anyone?

Examples of the Prisoner's Dilemma

Let's illustrate the classic prisoner's dilemma with the very same robbery situation:

Bonnie and Clyde robbed a bank, but were arrested and placed in different rooms for questioning. Unfortunately, the police have no other witnesses, making it incredibly difficult to prove Bonnie and Clyde's guilt unless one or both confess to it themselves. In the end, both robbers get presented with a choice: to keep silent, and then each gets only one year in prison, or to turn in the accomplice and go free, but then the accomplice gets the whole five years in prison. If they both confess, both Bonnie and Clyde get two years each.

Since Bonnie and Clyde are unaware of each other's decisions and act independently, there are four possible outcomes:

• Bonnie turns Clyde in and gets off scot-free, and Clyde goes to prison for five years.
• Clyde turns Bonnie in and goes free, while Bonnie goes to jail for five years.
• Clyde turns Bonnie in, and Bonnie turns Clyde in, and then both get two years in prison each.
• Clyde and Bonnie keep quiet, resulting in both getting only one year in prison.

In the survivor's dilemma, there is over a 50% chance of a third outcome, while a fourth outcome is only 5% likely to happen.

Also, consider examples of the Prisoner's Dilemma in real life, e.g., in business, where this dilemma occurs most often, exposing the whole market to risk. For example, suppose there are two cosmetics companies, and they are competitors. A price war flares up because both know that customers prefer the cheapest products. As a result, to attract as many customers as possible and stay ahead of the competition, both companies keep lowering their prices until they run at a disadvantage and into a deficit. In the end, neither of them gets any new customers, while the budget gets depleted, and profits are at zero.

The situation looks much the same in an arms race between different countries. The constant build-up of military power only serves to heighten fear and conflict in each other's societies, deplete resources and, instead of controlling the enemy, create even more complex international relations. The Prisoner's Dilemma can even arise in agriculture, where farmers constantly increase production and quantity, resulting in market oversupply, decreasing demand and prices, and the threat of bankruptcy.